Mathematical informatics lies at the heart of modern technology. It combines the precision of mathematics with the pragmatism of computer science, forming a backbone for algorithm design, data structures, optimization, and network analysis. Key pillars of this discipline—algorithms, graph theory, and combinatorics—work in concert to solve real-world computational problems. Understanding how these mathematical tools interact illuminates the structure of many systems in computing, telecommunications, logistics, and artificial intelligence.
Algorithms are step-by-step procedures or rules for solving problems. They allow us to transform input data into desired outputs efficiently. Good algorithm design is not merely about correctness, but about optimizing time complexity, memory consumption, and scalability. Mathematical informatics uses combinatorial and graph-theoretic thinking to analyze and improve these properties.
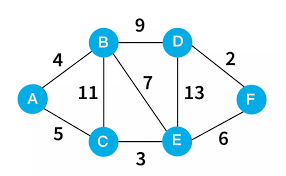
Graph theory studies nodes (vertices) and edges that connect them—an abstraction that can represent anything from computer networks and social media to transportation systems and molecular structures. By modeling systems as graphs, one can apply powerful mathematical theorems and algorithms (such as shortest path, matching, flows, connectivity) to make predictions, optimize resources, or detect vulnerabilities.
Combinatorics is the branch of mathematics dealing with counting, arrangement, and selection. In informatics, combinatorial methods enable us to enumerate possibilities, optimize configurations, and understand complexity. Problems such as scheduling, resource allocation, hashing, cryptography, and coding theory all rely on combinatorial insights.
By embedding combinatorial reasoning and graph models into algorithmic frameworks, mathematical informatics provides the theoretical tools and practical strategies to build and analyze technologies in a rigorous and efficient way.
 Algorithms and Combinatorics: Counting, Optimizing, and Searching
Algorithms and Combinatorics: Counting, Optimizing, and Searching
Combinatorics profoundly influences algorithm design. Many algorithms are fundamentally about exploring combinations, permutations, or subsets of a set, and doing so efficiently. Let us explore some key areas where combinatorial methods are central.
Search and Enumeration Algorithms.
Suppose we need to generate all possible combinations of features or configuration settings in a software system for testing. A brute‑force approach might enumerate (nk)\binom{n}{k} combinations (for choosing kk of nn settings). Combinatorial enumeration underlies backtracking algorithms, branch‑and‑bound techniques, and exhaustive search. But combinatorics also inspires pruning strategies: if you know the number of combinations, you can avoid redundant searches, skip symmetrical cases, or apply heuristics to focus on promising regions of the search space.
Optimization and Combinatorial Optimization.
Many real-world problems involve optimizing over a discrete domain: selecting the best subset, ordering tasks, or assigning resources. Classic combinatorial optimization problems include the Traveling Salesman Problem (TSP), knapsack problem, and minimum spanning tree. While some of these are NP-hard, approximation algorithms, dynamic programming, and greedy strategies (rooted in combinatorial reasoning) help tackle them in practice. For example, dynamic programming for TSP uses combinatorics to consider subsets of nodes, building optimal tours by combining smaller solutions.
Randomized Algorithms and Hashing.
Combinatorics also underlies randomized algorithms and data structures like hash tables. Universal hashing, for instance, depends on selecting hash functions such that the probability of collision is minimized. Combinatorial reasoning (about the number of possible hash functions, the size of the domain, and the expected number of collisions) helps ensure that the hash table performs efficiently on average. Similarly, randomized algorithms for primality testing, sampling, or load balancing rely on combinatorial probabilities to guarantee performance with high probability.
Complexity Theory and Counting Classes.
In theoretical computer science, combinatorics defines complexity classes such as #P (sharp‑P), which deals with counting the number of accepting paths of a nondeterministic polynomial-time machine. Problems in #P (like counting Hamiltonian cycles or perfect matchings) are combinatorial at their core. Algorithms for approximate counting, or reductions between counting problems, apply combinatorial identities (inclusion–exclusion principle, binomial coefficients) to reason about complexity and derive performance bounds.
Graph Theory in Technology: Modeling, Networks, and Infrastructure
Graph theory is one of the most powerful mathematical abstractions for modeling relationships and structures. In mathematical informatics, it plays a critical role in representing connections, optimizing flows, and analyzing networks.
Network Graphs and Communication.
In telecommunications, the internet, or peer-to-peer systems, nodes represent routers or devices, and edges represent connections or communication links. Routing algorithms, such as Dijkstra’s algorithm for shortest paths, Bellman–Ford, or more advanced protocols (like OSPF, BGP), rely on graph-theoretic principles. These algorithms compute optimal paths, minimize latency or cost, and dynamically adapt when links go down.
Flow Networks and Optimization.
Graphs with capacities on edges (flow networks) model real-life problems such as transportation, supply chains, and data flow. Maximum-flow algorithms (Ford–Fulkerson, Edmonds–Karp, Dinic’s) compute how much “flow” can go from a source to a sink in a network, subject to capacity constraints. These algorithms are foundational in logistics (maximizing cargo shipped), telecommunications (maximizing bandwidth), and even in bipartite matching problems like job assignments.
Graph Algorithms in Social and Biological Networks.
Graph theory helps analyze social networks (e.g., users in a social media platform) or biological networks (e.g., protein–protein interactions). Centrality measures (degree, betweenness, eigenvector centrality) identify influential nodes. Community detection algorithms (like modularity optimization, spectral clustering) reveal clusters or communities. These combinatorial and graph‑based techniques help in recommendation systems, epidemiological modeling, and bioinformatics.
Planar Graphs, Embedding, and Geographic Applications.
When modeling geographic or physical networks (like road systems, utility grids, or circuit layouts), planar graph theory becomes useful. Algorithms that operate on planar graphs can exploit their special properties (for example, via face traversal or dual graphs) to optimize routing, design, or layout. Combinatorial properties of planar graphs (like Euler’s formula V−E+F=2V – E + F = 2) help in designing efficient infrastructure and ensuring structural robustness.
Integrating Combinatorics and Graph Theory in Algorithms: Real-World Applications
The synergy between combinatorics, graph theory, and algorithm design manifests in many domains of technology. Here we illustrate how these mathematical foundations power modern systems.
Task Scheduling and Resource Allocation.
Consider a data center or a cloud platform where jobs (tasks) must be scheduled on machines. This is naturally modeled as a graph or bipartite matching problem: tasks and machines, edges indicating feasible assignments. Combinatorial algorithms (like the Hungarian algorithm) find optimal matchings, minimizing cost or maximizing throughput. When tasks have dependencies, the problem involves directed acyclic graphs (DAGs), and one often uses topological sort combined with cost optimization (e.g., dynamic programming over subsets) to schedule tasks efficiently.
Communication Networks and Resilience.
To ensure reliability, network designers often want to find minimum spanning trees (MST) for basic connectivity, and redundant paths for fault tolerance. Algorithms like Kruskal’s or Prim’s build MSTs by combinatorially selecting edges. For redundancy, one might compute k‑edge‑disjoint paths (using max-flow) to guarantee that even if some links fail, communication remains intact.
Coding Theory and Error Correction.
Error‑correcting codes (e.g., Reed–Solomon, LDPC, turbo codes) are grounded in combinatorial structures and graph theory. Tanner graphs represent codes, and belief propagation (on those graphs) decodes messages by combining local information. Combinatorial counting ensures that codes have sufficient distance (i.e., minimum Hamming distance), which determines how many errors can be detected or corrected.
Cryptography and Secure Communication.
Cryptographic protocols rely heavily on combinatorial problems. For example, the difficulty of factoring or discrete logarithm problems underpins public-key cryptography. Combinatorial reasoning also supports zero-knowledge proofs (selecting subsets, permutations) and hash-based signatures (counting possible hash functions). Graph-based cryptography (e.g., expander graphs) is used to design robust, high-throughput networks for secure communication.
Artificial Intelligence and Machine Learning.
Combinatorics and graph theory are central in many AI algorithms. Bayesian networks (directed acyclic graphs) model probabilistic dependencies; Markov decision processes (graph-based) plan sequences of actions. Graph neural networks (GNNs) implement deep learning directly on graph structures. Combinatorial optimization arises in feature selection, hyperparameter tuning, and ensemble learning (selecting subsets of models).
Table: Applications of Algorithms, Graphs, and Combinatorics in Technology
| Domain | Mathematical Tool | Application | Impact |
|---|---|---|---|
| Cloud & Scheduling | Matching (combinatorics) + DAGs | Task‑machine assignment, dependency scheduling | Optimized usage, reduced latency |
| Networks & Communication | Graph algorithms + flow theory | Routing, fault tolerance, bandwidth allocation | Reliable, efficient connectivity |
| Coding & Data Transmission | Tanner graphs + combinatorial design | Error‑correcting codes, decoding | Improved data integrity |
| Cryptography | Combinatorial counting + expander graphs | Secure protocols, zero‑knowledge proofs | High security, efficient key exchange |
| AI & ML | Bayesian networks, GNN, combinatorial optimization | Probabilistic models, graph learning, feature selection | Better predictions, structured learning |
Challenges, Trends, and the Future of Mathematical Informatics
While the integration of algorithms, graphs, and combinatorics has already driven significant technological advances, the field continues to face both challenges and exciting new trends.
Scalability and Big Data.
Modern data sets can be enormous: social networks with billions of edges, genomic graphs with millions of nodes, or combinatorial spaces so large they cannot be explicitly enumerated. Traditional combinatorial and graph algorithms may struggle at this scale, so research focuses on approximation algorithms, streaming graph algorithms, sketching techniques, and parallel/distributed computing. Combinatorial sampling and randomized algorithms help to approximate counts, flows, and matchings in massive data environments.
Quantum Computing and Combinatorial Problems.
Quantum algorithms promise to revolutionize combinatorial optimization. Algorithms like Grover’s search or quantum approximate optimization algorithm (QAOA) map combinatorial problems (e.g., max-cut, traveling salesman) to quantum circuits. Graph theory also plays a role in representing quantum entanglement and quantum communication networks, pushing the boundaries of both information theory and combinatorics.
Network Robustness and Dynamic Graphs.
Real-world networks evolve: edges appear and disappear, nodes join and leave. Dynamic graph theory studies how to maintain critical properties (connectivity, centrality, minimum cut) in such environments. Combinatorial algorithms for dynamic matching, incremental flow, and real-time graph updates are becoming essential for resilient infrastructures, especially in mobile networks, IoT systems, and distributed computing.
Privacy, Security, and Combinatorial Privacy.
Privacy-preserving technologies (like differential privacy) combine combinatorial reasoning with probabilistic algorithms. Graph anonymization (hiding graph structure while preserving utility) is a combinatorial challenge: how to permute, add, or delete edges to guarantee privacy without destroying the graph’s analytic value. Cryptographic protocols are also evolving to leverage combinatorial structures to minimize information leakage while maximizing efficiency.
Explainable AI and Graph-Based Interpretability.
Graph-based machine learning, like GNNs or knowledge graphs, is unlocking new ways to understand decision-making. Combinatorial reasoning helps to identify subgraphs, motifs, or feature subsets that drive predictions. These same techniques allow us to explain AI behavior, improve fairness, and audit model structure for biases.
Conclusion
Mathematical informatics—through the deep interplay of algorithms, graph theory, and combinatorics—is far more than an academic abstraction. It is the conceptual foundation of many of today’s most powerful technologies. From optimizing schedules in a data center to designing fault‑tolerant networks, from securing communication to enabling machine learning on relational data, the lessons of combinatorics and graph theory inform our digital world.
Algorithms count, enumerate, explore, and optimize; graphs model structure, connectivity, and flow; and combinatorics opens the door to counting possibilities, reasoning about complexity, and making informed decisions under constraints. Together, they provide a toolkit for building efficient, resilient, and intelligent systems.
As we move further into the age of big data, quantum computing, and distributed intelligence, the importance of mathematical informatics will only increase. Scalability, adaptability, and security remain central challenges, but because of the solid foundation laid by combinatorial mathematics and graph theory, we are well-equipped to meet them. By continuing to develop and apply these tools, we not only solve today’s problems—we unlock the technologies of tomorrow.