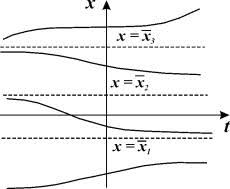
Differential equations are one of those mathematical tools that quietly stand behind many everyday phenomena. They describe temperature fluctuations in a room, the spread of epidemics, the oscillation of a spring, the growth and decline of populations, radioactive decay, motion, and even fluctuations in financial markets. Whenever a process changes continuously over time — mass, velocity, temperature, population size, concentration of a substance — differential equations serve as the language that mathematically captures these changes.
For beginners, understanding differential equations does not mean mastering complicated solving techniques. Instead, it means grasping the basic idea: a differential equation connects a quantity and the rate at which that quantity changes. It answers the central question: how does the system transform if its current state changes?
This essay explores the intuitive nature of differential equations, their basic types, and the most common models used to describe real-world processes: growth, decay, heat exchange, and oscillations.
Foundations: What a Differential Equation Is and Why It Matters
A differential equation (DE) is an equation involving derivatives of an unknown function describing a process. The derivative represents a rate of change.
In simple terms:
-
the function describes the state,
-
the derivative describes how fast the state changes,
-
the differential equation ties the two together.
This connection allows us to predict how a system behaves in the future.
The simplest example
A differential equation of the form
dydt=ky\frac{dy}{dt} = ky
means that the rate of change is proportional to the current value.
If k>0k > 0, the quantity grows; if k<0k < 0, it decays.
This simple model underlies many processes: bacterial growth, radioactive decay, early stages of information spread, financial interest, and temperature change.
Why we need models
The real world is too complex to describe every detail. Differential equations allow us to extract the essential law of change and work with simplified yet powerful descriptions of real systems.
This is why physics, biology, chemistry, economics, and engineering rely on differential equations as a fundamental modeling tool.
Models of Growth and Decay: From Exponential Patterns to Logistic Curves
Some of the most intuitive and widely used differential equation models are those that describe growth and decay. They are simple enough for beginners yet powerful enough to explain real phenomena.
Exponential growth
The equation
dydt=ky,k>0\frac{dy}{dt} = ky, \quad k>0
describes exponential growth, with the solution
y(t)=y0ekt.y(t) = y_0 e^{kt}.
Exponential growth occurs when resources are unlimited:
-
bacteria in fresh nutrient medium;
-
initial spread of a viral post on social media;
-
growth of capital with constant interest;
-
acceleration of chemical reactions in early phases.
Exponential decay
With k<0k < 0, the same equation describes decay:
dydt=ky,k<0.\frac{dy}{dt} = ky, \quad k<0.
This applies to:
-
radioactive decay;
-
cooling of objects;
-
depletion of resources;
-
removal of medication from the body.
Logistic growth
Exponential growth cannot continue forever. Logistic models introduce the idea of a carrying capacity — a maximum possible population size:
dydt=ky(1−yK).\frac{dy}{dt} = ky\left(1 – \frac{y}{K}\right).
This is a realistic model for population biology, marketing, the spread of technologies, and even audience growth.
Comparison of three key models
| Model | Equation | Applications | Key Feature |
|---|---|---|---|
| Exponential growth | dydt=ky\frac{dy}{dt} = ky, k>0k>0 | Populations, finance, information spread | Unlimited growth |
| Exponential decay | dydt=ky\frac{dy}{dt} = ky, k<0k<0 | Radioactive decay, cooling, resource depletion | Rapid decline toward zero |
| Logistic growth | dydt=ky(1−y/K)\frac{dy}{dt} = ky(1-y/K) | Biology, economics, marketing | Growth with saturation |
Even these simple models demonstrate how differential equations describe a broad range of natural and social phenomena.
Heat Transfer and Temperature Change: Newton’s Law of Cooling
One of the most widely known differential equations in physics is Newton’s Law of Cooling, which states that the rate of temperature change is proportional to the difference between the temperature of an object and the surrounding environment:
dTdt=−k(T−Tenv).\frac{dT}{dt} = -k (T – T_{\text{env}}).
If you place a hot kettle on the table, it will gradually cool down, approaching room temperature.
Why this model matters
Newton’s law is used in numerous fields:
-
forensic science (estimating time of death from body temperature);
-
engineering (evaluating cooling systems);
-
computer science (analyzing processor heating);
-
environmental science (studying heat exchange in ecosystems);
-
industrial design (preventing overheating of devices).
Intuition behind the model
The greater the temperature difference, the faster the heat exchange.
As the object cools, this difference becomes smaller, and the process slows.
Mathematically, this produces an exponential curve — a pattern captured perfectly by the equation.
Real-world accuracy
Despite its simplicity, Newton’s model is remarkably accurate for a variety of real systems, which is why it is a fundamental example in introductory differential equations courses.
Oscillatory Models: Harmonic Motion and Real-World Vibrations
Beyond growth and decay, many systems do not simply increase or decrease — they oscillate. These processes involve second derivatives, which describe acceleration.
The harmonic oscillator
The simplest model of oscillations is:
d2xdt2+ω2x=0.\frac{d^2x}{dt^2} + \omega^2 x = 0.
It describes:
-
spring–mass systems;
-
pendulums (at small angles);
-
electrical LC circuits;
-
mechanical vibrations;
-
acoustic waves.
Its solution is a sinusoidal function:
x(t)=Acos(ωt)+Bsin(ωt).x(t) = A\cos(\omega t) + B\sin(\omega t).
This model forms the basis of acoustics, optics, quantum physics, electronics, architecture, and even biological rhythms.
Damped oscillations
If friction or resistance is present, the model becomes:
d2xdt2+bdxdt+ω2x=0.\frac{d^2x}{dt^2} + b\frac{dx}{dt} + \omega^2x = 0.
The amplitude gradually decreases. This describes:
-
vehicle suspension systems;
-
guitar strings;
-
oscillation of building components;
-
sound waves in enclosed spaces.
Forced oscillations and resonance
If an external periodic force is applied to the system, it can enter resonance.
A famous example is the 1940 Tacoma Narrows Bridge collapse, caused by wind-induced resonance.
These dramatic real-world outcomes show the predictive power of differential equations.
Conclusion
Differential equations are not just abstract mathematical constructs but a precise language used to describe real-world behavior. Models of growth and decay explain how populations, resources, and temperatures change. Newton’s cooling law helps us understand heat dynamics in engineering, biology, and everyday environments. Oscillatory models describe vibrations, waves, and periodic processes across physics, engineering, and technology.
Despite their apparent complexity, the fundamental ideas behind differential equations are straightforward: they link the state of a system with the rate of its change. Understanding this relationship enables us to interpret natural processes, anticipate system behavior, and build more accurate scientific models.
Differential equations open the door to a deeper understanding of the world, making complex phenomena structured and predictable. For anyone interested in science, technology, or the mechanisms underlying daily life, they provide one of the most powerful analytical tools available.