At first glance, mathematics and biology may seem like entirely separate fields, but their interaction opens unique opportunities to study nature, predict processes, and make decisions in ecology, medicine, and agriculture. Modern biology increasingly relies on quantitative methods: numerical models allow researchers to describe population growth, infection spread, ecosystem dynamics, and the impact of environmental factors on living organisms.
One of the key areas where mathematics is applied in biology is population modeling. Already in the early 20th century, biologists and mathematicians began using simple equations to describe the number of animals, plants, and microorganisms. These models enabled predictions of how populations would change over time depending on resources, environmental conditions, and interactions with other species.
Population Growth Models
Population growth in biology is often described using two classical models: exponential and logistic. Exponential growth assumes that each individual contributes equally to the population increase and that resources are unlimited. It is described by the equation:
dNdt=rN\frac{dN}{dt} = r N
where NN is population size, tt is time, and rr is the growth rate. This model is suitable for the initial stages of colonizing a new habitat or bacterial reproduction under favorable conditions. However, real environments are limited, and unlimited growth is impossible.
To account for environmental constraints, the logistic growth model is used:
dNdt=rN(1−NK)\frac{dN}{dt} = r N \left(1 – \frac{N}{K}\right)
where KK is the carrying capacity, the maximum population that the ecosystem can sustain. This model reflects the slowing of growth as the population approaches the resource limit and allows predictions about ecosystem stability.
The logistic model has practical applications: it helps agriculture plan planting densities, conservationists predict endangered species numbers, and ecologists simulate competition between species.
Mathematics in Ecology
Mathematical methods in ecology help describe complex interactions between species and their environment. A critical task is understanding predator-prey dynamics, such as wolves and deer in forest ecosystems. The classical Lotka–Volterra model describes these interactions with a system of differential equations:
dxdt=αx−βxy\frac{dx}{dt} = \alpha x – \beta xy dydt=δxy−γy\frac{dy}{dt} = \delta xy – \gamma y
where xx is prey population, yy is predator population, and α,β,γ,δ\alpha, \beta, \gamma, \delta are coefficients determining reproduction, predation, and mortality rates.
These models allow prediction of population oscillations, assessment of ecosystem stability, and evaluation of human interventions such as hunting, species protection, or establishing reserves. More complex models consider multiple species, migration, seasonal changes, and environmental stresses.
 Mathematical Models of Epidemics
Mathematical Models of Epidemics
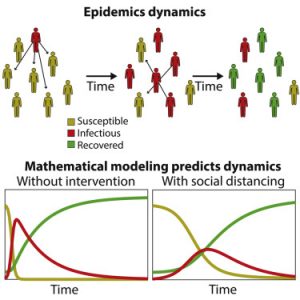
Another field where mathematics is crucial is epidemiology — the study of disease spread. Mathematical models aim to predict the dynamics of infections and assess the effectiveness of prevention measures.
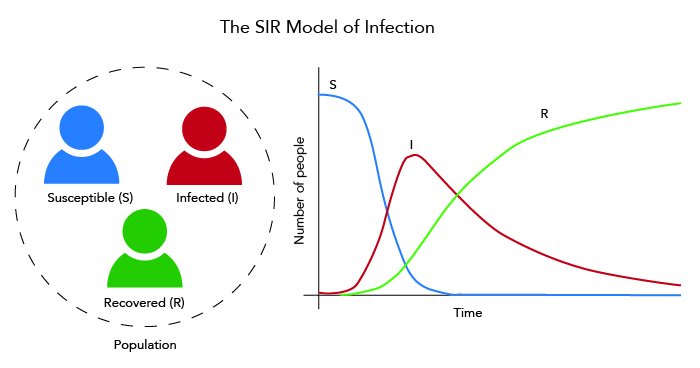
The classic SIR model divides the population into three groups: Susceptible (S), Infected (I), and Recovered (R). The model is expressed as:
dSdt=−βSI\frac{dS}{dt} = – \beta S I dIdt=βSI−γI\frac{dI}{dt} = \beta S I – \gamma I dRdt=γI\frac{dR}{dt} = \gamma I
where β\beta is the infection transmission rate and γ\gamma is the recovery rate. This model helps predict the peak load on healthcare systems, estimate epidemic durations, and evaluate vaccination strategies.
Modern epidemiological models are often more complex, incorporating age groups, contact networks, seasonal effects, vaccination, and viral mutations. Mathematics enables informed decisions on lockdowns, social distancing, and mass vaccination, making epidemic management scientifically grounded.
Applications of Statistics and Probabilistic Models
Mathematics in biology extends beyond differential equations. Statistics and probability theory are crucial for analyzing experimental data, estimating populations, predicting rare events, and studying genetics.
For instance, probabilistic models are used to study trait inheritance, predict mutation spread, and model genetic diversity. Regression and correlation methods help analyze population dependence on environmental factors, climate, or human activity.
In ecology, probabilistic approaches assess the risk of species extinction, analyze invasive species spread, and simulate random events such as wildfires or droughts. In epidemiology, probability models estimate infection likelihood, outbreak probability, and optimize vaccination strategies.
Practical Examples
Mathematical models are applied across many areas of biology. In agriculture, the logistic growth model helps plan planting density, forecast yields, and optimize resource use. In fisheries, predator-prey models determine sustainable harvest levels to maintain ecosystem stability.
In medicine, epidemic models inform vaccination planning and infection spread forecasts. SIR models have been applied to influenza, measles, and more recently, COVID-19, aiding decisions on quarantine measures, mass vaccination, and social contact restrictions.
More advanced models, such as SEIR (including an Exposed group), account for the latent period of disease and allow more precise epidemic predictions.
Table: Key Mathematical Models in Biology
| Model | Application | Main Equations | Practical Use |
|---|---|---|---|
| Exponential Growth | Populations without limits | dNdt=rN\frac{dN}{dt} = r N | Bacterial colonies, early reproduction stages |
| Logistic Growth | Populations with limited resources | dNdt=rN(1−NK)\frac{dN}{dt} = r N (1 – \frac{N}{K}) | Forecasting plant and animal populations |
| Lotka–Volterra | Predator-prey dynamics | dxdt=αx−βxy;dydt=δxy−γy\frac{dx}{dt} = \alpha x – \beta xy; \frac{dy}{dt} = \delta xy – \gamma y | Ecosystem stability, population management |
| SIR | Infectious disease spread | dSdt=−βSI;dIdt=βSI−γI;dRdt=γI\frac{dS}{dt} = -\beta SI; \frac{dI}{dt} = \beta SI – \gamma I; \frac{dR}{dt} = \gamma I | Epidemics, vaccination, infection forecasts |
| SEIR | Epidemics with latent period | Adds Exposed group E | More accurate epidemic modeling |
| Probabilistic Models | Genetics, rare events | Varies per case | Trait inheritance, extinction risk, mutation spread |
Conclusion
Applying mathematics in biology allows for a deeper understanding of processes in living systems, predicting their dynamics, and developing strategies for ecosystem and disease management. Differential equations, probabilistic models, and statistical methods provide precise quantitative estimates that assist ecologists, farmers, and medical professionals.
Population growth, predator-prey interactions, and disease spread can all be described mathematically, offering opportunities for forecasting and optimization. Mathematical models give scientists and practitioners tools for informed decisions, risk minimization, and resource management.
Modern biology is increasingly quantitative and analytical, with mathematics serving as a universal language for describing complex life processes. Mastering these methods is essential for specialists, students, and educators, as it develops analytical thinking, data interpretation skills, and understanding of natural patterns.
The interaction of mathematics and biology not only enables the study of life but also contributes to its preservation, human health, and ecosystem sustainability. Through modeling and analysis, it is possible to make practical, science-based decisions that benefit both nature and society.