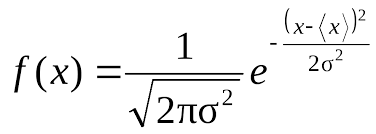
The history of mathematics is, in many ways, the history of human reasoning itself. It reflects humanity’s continuous attempts to understand the patterns of nature, to formalize abstractions, to capture the structure of space, and to describe the infinite. Every major mathematical breakthrough is not simply a collection of formulas — it is a conceptual leap that reshapes science, technology, and our worldview.
Among the many figures who determined the trajectory of mathematical development, three stand out with exceptional influence: Carl Friedrich Gauss, Leonhard Euler, and Bernhard Riemann. Their theorems, methods, and philosophical approaches laid the foundation for modern number theory, analysis, geometry, and mathematical physics. Their discoveries continue to drive progress in engineering, computer science, cryptography, cosmology, and data analysis.
Gauss: The Birth of Modern Mathematical Rigor
Carl Friedrich Gauss — often called the prince of mathematicians — contributed to nearly every mathematical field. His work became the standard of proof, precision, and formal structure for the centuries that followed.
The Fundamental Theorem of Algebra
One of Gauss’s key contributions is the first fully rigorous proof of the Fundamental Theorem of Algebra, which states:
Every non-constant polynomial with complex coefficients has at least one complex root, and a polynomial of degree n has exactly n roots (counting multiplicities).
In the early 19th century, this statement was far from obvious. Complex numbers were widely considered a suspicious abstraction, lacking “real” meaning. Gauss, however, demonstrated that their existence is not optional — it is a mathematical necessity.
This theorem provided:
-
a stable foundation for complex analysis,
-
a bridge between algebra and geometry,
-
a rigorous basis for polynomial theory.
Intrinsic Curvature and the “Theorema Egregium”
In differential geometry, Gauss proved the remarkable Theorema Egregium, establishing that curvature is an intrinsic property of a surface. That is, curvature can be computed entirely from measurements within the surface, without reference to how it sits in a higher-dimensional space.
This idea ultimately enabled the development of Einstein’s general theory of relativity, where gravity is interpreted as curvature of spacetime.
Impact on Modern Science
Gauss’s insights underpin:
-
GPS and geodesy,
-
statistical theory and the Gaussian distribution,
-
electromagnetism,
-
celestial mechanics and orbital prediction,
-
financial mathematics and risk modeling.
His work did not simply expand mathematics — it helped establish the culture of mathematical rigor itself.
 Euler: The Mathematician Who Unified Entire Fields
Euler: The Mathematician Who Unified Entire Fields
Leonhard Euler remains the most prolific mathematician in history: nearly a third of all 18th-century mathematics is attributed to him. His work shaped the notation, structure, and conceptual unity of modern mathematics.
Euler’s Identity: The “Queen of Formulas”
Euler’s identity
eiπ+1=0e^{i\pi} + 1 = 0
is frequently cited as the most elegant equation ever written. It ties together the fundamental constants:
-
ee,
-
ii,
-
π\pi,
-
1,
-
and 0.
Beyond beauty, this formula created a conceptual bridge between:
-
exponential growth,
-
oscillations,
-
complex numbers,
-
trigonometric functions.
It became the backbone of:
-
quantum mechanics,
-
electrical engineering,
-
Fourier analysis,
-
signal processing,
-
cryptography,
-
wave theory.
The Birth of Graph Theory
Euler solved the famous Königsberg Bridges Problem, introducing the concept of a graph — a structure of vertices and edges. This single insight launched an entirely new field.
Today, graph theory is essential to:
-
internet structure and routing,
-
social network analysis,
-
logistics and optimization,
-
artificial intelligence and neural networks,
-
epidemiology and network-based disease modeling.
Euler showed that mathematics could describe not only numbers and shapes, but relationships — a foundational idea in the age of data and connectivity.
Euler and Physics
Euler’s equations of fluid dynamics still govern:
-
aerodynamics,
-
ocean currents,
-
atmospheric modeling,
-
plasma physics.
Modern engineering relies heavily on Euler’s analytical formulations.
Riemann: Geometry, Space, and the Rise of Mathematical Modernity
Bernhard Riemann revolutionized geometry, analysis, and number theory. His work introduced concepts that only became fully appreciated decades later, when physics and advanced mathematics caught up.
Riemannian Geometry and Curved Spaces
In his groundbreaking 1854 habilitation lecture, Riemann introduced the concept of what we now call Riemannian manifolds — spaces where curvature may vary from point to point, and which can have any number of dimensions.
This invention transformed mathematics and physics:
-
Einstein used Riemannian geometry to describe gravity.
-
Modern cosmology uses it to model the universe.
-
String theory uses higher-dimensional manifolds.
-
Machine learning relies on geometric data structures.
-
Topology and differential geometry became central areas of research.
Riemann changed not just our understanding of geometry, but our understanding of space itself.
The Riemann Hypothesis
In number theory, Riemann formulated his famous hypothesis about the non-trivial zeros of the zeta function lying on the critical line. It remains one of the Millennium Prize Problems and one of the deepest unsolved questions in mathematics.
A proof (or counterexample) would have vast implications for:
-
cryptography,
-
prime number theory,
-
algorithmic efficiency,
-
mathematical logic.
Impact on Modern Technology
Riemann’s ideas permeate:
-
encryption and cybersecurity,
-
GPS and differential geometry applications,
-
quantum field theory,
-
data analysis on manifolds,
-
theoretical physics.
His work expanded the very framework within which mathematics describes reality.
Table: Key Mathematical Discoveries and Their Modern Impact
| Mathematician | Major Contribution | Scientific Importance | Modern Applications |
|---|---|---|---|
| Gauss | Fundamental Theorem of Algebra; intrinsic curvature | Foundation of complex analysis and differential geometry | GPS, statistics, physics, finance |
| Euler | Euler’s identity; graph theory | Unification of mathematical fields; emergence of network theory | Internet, ML, electrical engineering |
| Riemann | Manifold geometry; Riemann Hypothesis | New concept of space; core of number theory | Cosmology, cryptography, quantum physics |
Conclusion: Mathematics as the Engine of Civilization
The great theorems of Gauss, Euler, and Riemann are not merely proofs — they are foundational ideas that shape the structure of modern science. They gave humanity tools to describe the universe, creating the intellectual framework for physics, engineering, technology, and the digital world.
Without their contributions, there would be no:
-
modern physics,
-
computer networks,
-
advanced navigation systems,
-
cryptography and cybersecurity,
-
data science,
-
geometric analysis.
These mathematicians did not simply solve problems — they created the methodologies through which problems can be solved. Their legacy forms the mathematical backbone of contemporary civilization.